The Wonder and Amusement of Triangles - Part Two, the Law of Missing Lengths
Who stole my Thunder ?
The next stage in our five year mission to explore strange new worlds, is a look at what I call the Law of Missing Lengths. I came up with the formulae for these goodness knows how, but it was from a number of similar questions which involve an unknown length, and you have to solve it in a roundabout way using the Law of Sines, and such forth, so I wondered if it could be done a better way. Again, if you want to see how I arrived at the formulae here presented, I don’t really have a clue, because when I get into a creative rush, my notes end up all over the place. I tend to find a formula the long way round, then realise only later that it could have been done even easier. But never mind. I shall show you a diagram, and slowly take you through the steps to prove the equations I have come up with are valid.
To illustrate the Law of Missing Lengths - done by Chris Lilly on Paintbox™
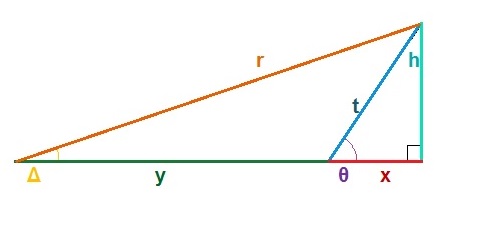
Concerning the Diagram above
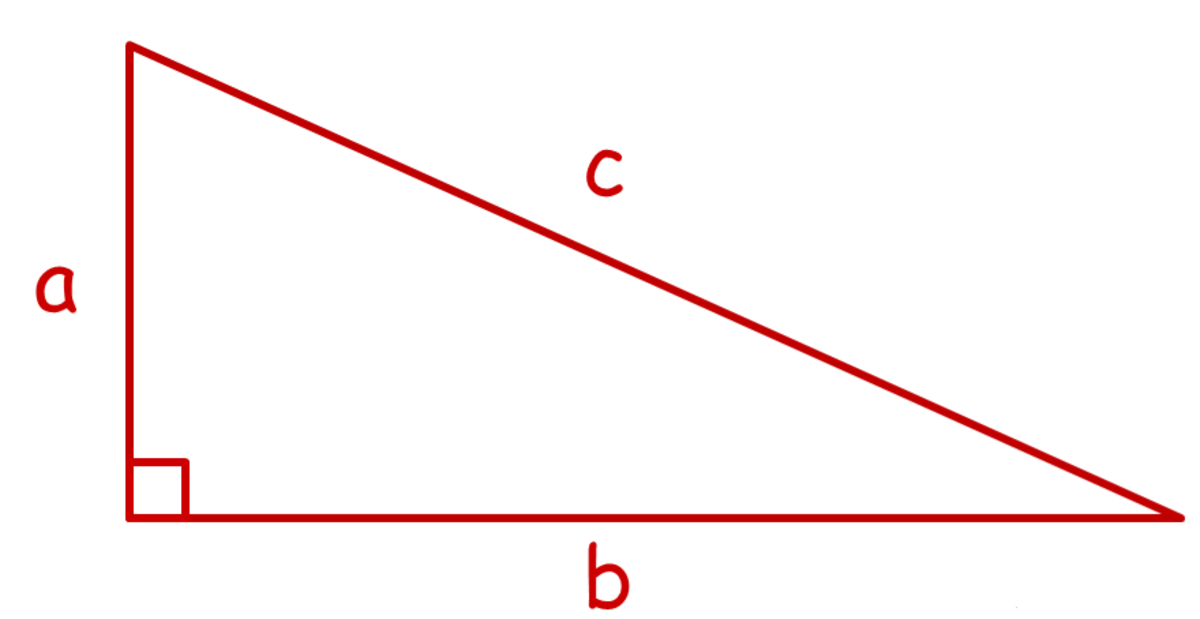
We see here a triangle with two relevant angles, θ and Δ, and given one or both, you may be asked to find out the lengths of any of the line segments on the triangle. Naturally in order to do so, you do have to know at least one of those lengths, otherwise, due to the idea of the similarity of triangles, the triangle in question could be to any scale, and given no lengths, you wouldn’t even know if it is in inches, feet or miles.
If we look at the angles with respect to the given lengths, we can see that tan Δ = h ÷ ( y + x ), and also that tan θ = h ÷ x. What I shall do next is show the formulae I have discovered, and then I shall prove their validity using the above relationships.
Formulation drawn by Chris Lilly on Paintbox™

On the Formulae for the Law of Missing Lengths
Now all this may seem a bit confusing, but if you follow the logic of changing the subject of any given formula, you will see how each of these equations are consistent with each other. The key now is to make them agree with our first observations, that tan Δ = h ÷ ( y + x ), and tan θ = h ÷ x, since these are more obvious, from which then we know them to be true.
Proof the formula works by Chris Lilly on Paintbox™

Commenting on the result above
So this proves the first equation was right, and that x was equal to what we thought it was. Now since I have proved that one of the formulae I devised agrees with observations about the value of the tangents with respect to the lengths ( that is, that tan θ = h ÷ x, and tan Δ = h ÷ ( y + x ) ), all I need to prove is that this formula I have shown to be correct agrees with all the others I have proposed, meaning also that I do not need to prove another of my formulae in the way I have just done. In spite of that, I will do so anyway, as a kind of double proof, so as to leave us in no doubt. First of all, another formula :
Proof of the formula for h, illustrated by Chris Lilly on Paintbox™

So having proven that two of the formulae are consistent when the Tangents are given their fractional length ratio values, let us then compare these formula to each other, to see if they agree in that way, which would prove their validity.
The third formula in line is the following for y :
Done by Chris Lilly on Paintbox™

This is just a rearrangement of the one proven above for h.
Since h = ÷ ( tanθ – tan Δ), then we can make y the subject by realizing this means that h ( tanθ – tan Δ) = y (tan Δ tan θ) and go on to say that
h ( tanθ – tan Δ) ÷ (tan Δ tan θ) = y.
The next length to consider is r, which forms the hypotenuse of the larger right angled triangle, this being the longest length in the whole diagram.
Formula for the Side known as r, by Chris Lilly on Paintbox™

Now based on the first diagram for this Hub, and from what is also noted in the illustration just above, we can see and are told that h ÷ r = sin Δ, since h ( meaning height ) is the opposite side to the angle Δ, and r is its hypotenuse. Because h ÷ r = sin Δ, then h = r sin Δ, and r = h ÷ sin Δ.
This here is a simple form of the equation, but what if we didn’t have the value of h, and only instead had that of y ? We would need to incorporate my formula for h involving y into this simple one, and since we have shown that h = ( y tan Δ tan θ ) ÷ ( tan θ - tan Δ ), we can express it as :
r = [ ( y tan Δ tan θ ) ÷ ( tan θ - tan Δ ) ] ÷ sin Δ, exactly the way I have in the illustration above of my formula for r, by placing sin Δ in the appropriate manner into the denominator of the fraction.
This is a little thought about the characteristics of fractions, ignorance of which may lead to errors in calculation, where if a second term is to be placed into the denominator, such that what is in the numerator is to be divided thereby also, it joins the original term and shall be multiplied by it, and it is this new combined product value that the numerator is to be divided by.
For example, if we had the equation 25 = ( 100 ÷ 2 ) ÷ 2, which of course can be rewritten 25 = ( 50 ) ÷ 2, the relationship can also be expressed by writing it all out as 25 = [ 100 ÷ ( 2 × 2 ) ], which we also know to be true, so that, when outside of the fraction the extra term is to be divided, when it enters the denominator, it is to be multiplied, and note the change in position of the parentheses. If these ideas are confusing, when looking at a fraction, carefully consider what it is trying to say, and work from there. There is also a previous Hub on Fractions at The Maths They Never Taught Us - Part Three , the Section entitled There's a Fraction too much Fraction.
Last not Least
The last length we have here is t. This is the hypotenuse of the smaller of the two right angled triangles, and once we look at it, we can see that
t time, drawn by Chris Lilly on Paintbox™

In Summary
So there we have it. From a triangle formed in the manner shown within another triangle, as long as we know both angles, and at least one side, we can work out all the other sides using the formulae shown, and if we have more than one side but only one angle, the other angle can be figured out by rearranging the relevant formula. If we know all sides but none of the angles, we should be able to figure them both out using as many of these four formulae as we need. The formulae then are as follows :
Four of the Formulae for the Law of Missing Lengths, by Chris Lilly on Paintbox™
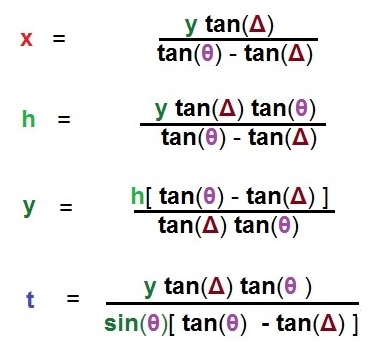
Par Example
Let us check this out by taking an example, and seeing if the formulae given agree with other Mathematical Laws we know.
Completed by Chris Lilly on Paintbox™
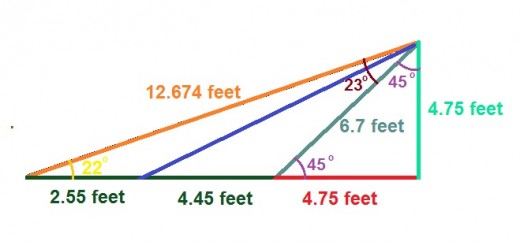
Isn’t this a nasty little toe wipe ? The 23° angle includes both smaller angles put together, made at where the hypotenuse of the largest triangle joins to the vertical height. The unknown angle is the middle one along the base, stemming from which is the unknown length that goes up to cut the 23° angle into its two parts.
What we are to do here, is to ignore the innermost 45° angle on the base as if it never existed, so that in keeping the same nomenclature, we call the unknown angle, now the inner one closer to the right angle, θ, and then the one at far left is once again referred to as Δ, as shown in the adjusted illustration below.
Revised by Chris Lilly on Paintbox™
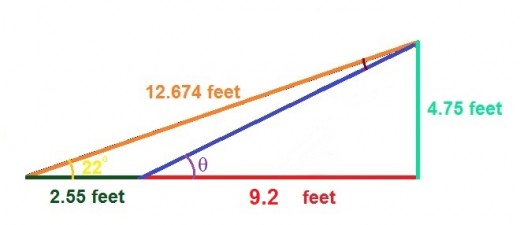
We then add the two lengths from θ to the right angle together : 4.45 + 4.75 = 9.2, which is designated as x, while the remaining length along the base, 2.55, corresponds to y. We apply my formula for finding x :
x = y tan Δ ÷ ( tan θ - tan Δ ), and substitute our values into it : 9.2 = 2.55 tan 22° ÷ ( tan θ - tan 22° )
From here we need to isolate tan θ, making it the subject of a formula equating it to values we can work out : 2.55 tan 22° ÷ 9.2 = ( tan θ - tan 22° ), if we then rearrange this : tan θ = 2.55 tan 22° ÷ 9.2 + tan 22°
Then we allow tan 22° to become part of our fraction and multiply it by 9.2, then place it on the numerator :
tan θ = ( 2.55 tan 22° + 9.2 tan 22° ) ÷ 9.2, after which we add like terms : tan θ = 11.75 tan 22° ÷ 9.2 = .516, and this means that the angle θ = 27° 17’ 59”.
To confirm this we can also see that tan θ = 4.75 ÷ 9.2, which is also equal to .516, so we have it right.
Now as for the unknown length, which in my diagrams is given the letter t, we know from a while ago that t = x ÷ cos θ, which also equals, by my formula : y tan Δ tan θ ÷ [sin θ (tan θ – tan Δ ) ], but just for fun, let’s use the first one :
x = 9.2, cos θ = .8885, therefore t = 10.35
The formula I have devised here are also consistent with the very complicated compound angle formulae, which we shall take a look at soon, just after we ponder the cosine, sine and tangent laws, next.
Disclaimer
As much as some of this Hub contains certain Mathematical knowledge accessible in the public domain, and not subject to any Copyright, other information has been drawn from textbooks which themselves are Copyright, but only in the sense of how they deliver the information which itself is shared and sometimes ancient Mathematical knowledge. Other information has also been found on Wikipedia ( Copyright 2013, the Wikimedia Foundation ), which is a good source of information. Part of this is also my own discovery, but may also independently have been found by others.
Who Stole My Thunder ? comes from a quote by one John Dennis ( 1658 - 1734 ), who had wanted to invent a thunder machine, but found one already at work in a theatre he had gone to in order to watch a play, the theatre whose managers he was said to have told of his idea, and therefore he thought they had stolen his idea - or that is to say, his thunder.
The Last, Not Least is a paraphrase of Last but not Least, which is inspired from the Bible, where in in Matthew 19:30 in John Wyclif's version of 1382, we find : But manye schulen be, the firste the laste, and the laste the firste. The quote is also seen in John Lyly's Euphues and His England, 1580.
Some of the illustrations in this particular Hub are my own, and have primarily been done using Microsoft™ Paintbox, edited from illustrations done using Microsoft™ Word. Others are, as noted, from Wikipedia. Any quote or part of this material which seems to belong to any other author should be treated as such, and I claim no ownership of anything I did not myself invent or discover, nor of any obvious copyright, trade mark, or registered trade mark.
The Adventure continues in the next Hubs, which continue the study of Triangles, and these are : The Wonder and Amusement of Triangles – Part Three : the Sine Rule, and The Wonder and Amusement of Triangles - Part Four : the Cosine Rule.
If You are curious, then do not hesitate to take a good look at the other Hubs, The Maths They Never Taught Us - Part One, The Maths They Never Taught Us - Part Two , The Maths They Never Taught Us - Part Three, The Very Next Step - Squares and the Power of Two , And then there were Three - a Study on Cubes, Moving on to Higher Powers - a First look at Exponents, The Power of Many More - more on the Use of Exponents, Mathematics - the Science of Patterns , More on the Patterns of Maths , Mathematics of Cricket , The Shape of Things to Come , Trigonometry to begin with , Pythagorean Theorem and Triplets, Things to do with Shapes, Pyramids - How to find their Height and Volume, How to find the Area of Regular Polygons, and The Wonder and Amusement of Triangles - Part One.
Also, feel free to check out my non Maths Hubs :
Bartholomew Webb , They Came and The Great New Zealand Flag
There will also be many More to come on a wide variety of Subjects.
Just take a good look at it, and note how interesting it all is, then see if you can come up with anything else along the same lines. As usual, I would appreciate any comments, feedback and suggestions which would be given due credit, or indeed have a go and publishing Your ideas Yourselves, but firstly, by all means, add Your comments - it's a free Country.